EfficientNet1. 딥러닝 논문의 구조
- 오늘의 이야기는 가장 유명한 딥러닝 기반 컴퓨터 비전 모델 중 하나로 꼽히는 ResNet의 논문으로 시작한다.
- ResNet 논문은 Residual Block이라는 아주 간단하면서도 획기적인 개념을 도입하여 딥러닝 모델의 레이어가 깊어져도 안정적으로 학습되면서 모델 성능 개선까지 가능함을 입증했다.
- 딥러닝 분야에서 사용되는 많은 기법들은 논문을 통해서 공개되는 경우가 많다.
- 논문에서 ResNet의 잔차 학습을 어떤 과정으로 소개하고 효과를 증명했는지는 딥러닝도 컴퓨터 과학의 한 분야이기 때문에, 실험을 통해 보여준다.
- 그래서 논문이 제안하는 새로운 방식과 효과를 확인하기 위해서는 어느 정도 논문의 구조를 파악하고 이해할 수 있어야 한다.
- 아래 그림은 간략한 논문이라는 구조를 파악하기 위해 삽입했다.

- 논문의 형식적 구조
1) 논문은 평소에 읽는 책과는 다르게 정형화된 형식을 가지고 있다.
2) abstract : 아이디어를 제안하는 방식과 학계에 이 논문이 기여하는 점을 요약한다. 그 뒤로는 논문의 주요 내용이 따라온다.
3) 논문 내용은 일반적으로 서론(introduction)과 관련 연구(related work), 그리고 소제목의 표현방식에 따라 달라지지만 일반적으로 제안하는 방법에 관한 이론 설명이 따라온다.
4) 이렇게 제안하는 방법을 소개한 후 효과를 확인하기 위한 실험(experiments) 셋팅과 결과가 따라 붙는다.
5) ResNet 논문에는 없지만 그 뒤로 결론(conclusion)으로 연구 내용 요약과 추가적인 연구방향을 소개하기도 한다.
6) 논문의 내용이 끝나면 뒤로는 참고문헌(reference)와 부록(appendix)가 붙는다.
7) 참고문헌에서는 논문의 설명과 구현에 있어 인용한 논문들의 리스트가 소개되고 부록에서는 미처 본문에서 설명하지 못한 구현이나 또는 추가적인 실험 설명이 포함된다.
- 이러한 논문의 형식 속에 담고자 하는 논리 구조가 있다.
1) 이전까지의 연구가 해결하지 못했던 문제의식
2) 이 문제를 해결하기 위한 그동안의 다른 시도들
3) 이 문제에 대한 이 논문만의 독창적인 시도
4) 그러한 시도가 가져온 차별화된 성과
2. ResNet의 핵심개념과 그 효과
- ResNet 논문의 문제의식
1) 서론(Introduction)을 통해 ResNet 논문이 제기하고 있는 문제의 핵심을 명확히 정리해 보자.
2) 최초로 제기한 질문은 딥러닝 모델의 레이어를 깊이 쌓으면 항상 성능이 좋아지는가 이다.
3) 이 질문이 문제의 핵심은 아니다.
4) 레이어를 깊이 쌓았을 때 Vanishing / Exploding Gradient 문제가 발생하여 모델의 수렴을 방해하는 문제가 생기는데, 여기에 대해서는 이미 몇가지 대응 방법이 알려져 있다.
5) 가장 눈에 띄는 키워드는 Degradation Problem이라는 표현이다.
6) 이것은 모델의 수렴을 방해하는 Vanishing / Exploding Gradient 문제와는 달리, 레이어를 깊이 쌓았을 때 모델이 수렴하고 있음에도 불구하고 발생하는 문제이다. 아래의 그래프가 이 문제를 보여준다.

7) Degradation Problem이란 어떤 현상인가?
(1) 딥러닝 모델의 레이어가 깊어졌을 때 모델이 수렴했음에도 불구하고 오히려 레이어 개수가 적을 때보다 모델의 training / test error가 더 커지는 현상이 발생하는데
(2) 이것은 오버피팅 때문이 아니라 네트워크 구조상 레이어를 깊이 쌓았을 때 최적화가 잘 안되기 때문에 발생하는 문제이다.
- ResNet 논문이 제시한 솔루션 : Residual Block
1) ResNet은 깊은 네트워크의 학습이 어려운 점을 해결하기 위해서 레이어의 입력값을 활용하여 레이어가 residual function(잔차 함수)을 학습하도록 한다.
2) 위 문구는 논문 abstract의 설명을 번역한 말이라 어려울 수 있다.
3) 단순하게는 일종의 지름길(shortcut connection)을 통해서 레이어가 입력값을 직접 참조하도록 레이어를 변경했다고 보면 된다.
4) Shortcut connection은 앞에서 입력으로 들어온 값을 네트워크의 출력층에 곧바로 더해준다.
5) 네트워크는 출력값에서 원본 입력을 제외한 잔차(residual) 함수를 학습하기 때문에 네트워크가 ResNet이라는 이름을 가지게 되었다.
6) 과연 레이어를 많이 쌓았다고 해서 모델 성능이 떨어지는 것을 어떻게 설명해야 할까? 저자들은 이 부분에 의문을 품었다.
7) 만약 기존 모델에다가 identity mapping 레이어를 수십장 덧붙인다고 해서 모델 성능이 떨어질 리 없을텐데, 그렇다면 레이어를 많이 쌓았을 때 이 레이어들은 오히려 identity mapping 레이어보다도 못하다는 뜻이 된다.
8) 많이 곂쳐 쌓은 레이어가 제대로 학습이 이루어지지 않았다는 반증이 된다.
9) 여기서 저자들은 기발한 생각을 한다. 학습해야 할 레이어 H(x)를 (F(x) + x)로 만들면 어떻게 되나? 여기서 x는 레이어의 입력값이다.
10) 그렇다면 F(x)가 Vanishing Gradient 현상으로 전혀 학습이 안되어 zero mapping이 되더라도, 최종 H(x)는 최소한 identity mapping이라도 될테니 성능 저하는 발생하지 않게 된다.
11) 그렇다면 실제로 학습해야 할 F(x)는 학습해야할 레이어 H(x)에다 입력값 x를 뺀 형태, 즉 잔차(Residual) 함수가 되는데, 이것은 H(x)를 직접 학습하는 것보다 훨씬 학습이 쉽지 않을까 하는 것이다.
12) 레이어를 깊이 쌓을수록 Residual에 해당하는 F(x)는 0에 가까운 작은 값으로 수렴해도 충분하기 때문이다.
13) 실험을 해보니 이 구조가 실제로도 안정적으로 학습이 되며, 레이어를 깊이 쌓을수록 성능이 향상되는 것이 확인되었다.
14) 정리하면, Residual 레이어를 F(x)로 표현하면 이 레이어의 결과는 입력값 x에 대해 F(x)가 된다.
15) 여기에 레이어의 입력값 x를 더해주면 최종 출력값은 (F(x) + x), 즉 우리가 보통 생각하는 레이어의 결과값이 된다.
16) 이후 이 값은 ReLU 활성함수(activation function)을 거치게 된다.
17) 논문에서 나오는 식에서 (F(x, W))는 학습되어야 할 residual mapping으로서 잔차 학습(residual learning)은 이 식을 학습한다.
18) ResNet에서는 shortcut connection을 가진 ResNet의 기본 블록을 Residual Block이라고 부른다. ResNet은 이런 Residual Block 여러 개로 이루어졌다.
19) 이런 shortcut connection의 아이디어는 다양한 레이어에 적용 가능하기 때문에 이후 나온 여러 네트워크 아키텍쳐에서 활용된다.
20) 블록(block)이란 무엇인가?
(1) 딥러닝 모델은 말 그대로 깊기 때문에, 깊은 네트워크를 쌓는 과정에서 레이어를 쌓는 패턴이 반복되기도 한다.
(2) 반복되는 레이어 구조를 묶고, 각 구조 속에서 조금씩 바뀌는 부분은 변수로 조정할 수 있게끔 만들면 레이어 구조를 바꾸며 실험을 할 때에도 편리할 것이다.
(3) 레이어를 묶은 모듈을 블록이라 부르며, 일반적으로 조금씩 변형을 준 블록을 반복적으로 쌓아 딥러닝 모델을 만든다.
- Experiments
1) 간략히 살펴보았듯 딥러닝 논문에서는 모델의 설계를 설명한 뒤 모델을 실제로 구현해 그 효과를 입증한다. ResNet을 예시로 논문의 실험(experiments) 부분을 조금 더 자세히 살펴본다.
2) ResNet에 추가된 shortcut connection의 아이디어를 검증하려면 어떤 실험을 해야 할까? 당연히 shortcut connection이 없는 네트워크와 이를 사용한 네트워크의 성능을 비교하면 된다.
3) 실제 논문에서는 네트워크가 깊어짐에 따라 발생하는 경사소실(vanishing gradient) 문제를 ResNet이 해결함을 보여주기 위해서, shortcut connection의 유무와 네트워크 깊이에 따라 모델을 나누어 구현한다.
4) 18개 층과 34개 층을 갖는 네트워크를 각각 shortcut이 없는 일반 네트워크(plain network)와 shortcut이 있는 ResNet 두 가지로 구현해 총 4가지를 만들었다. 이후 이미지넷(ImageNet) 데이터를 사용해 효과를 분석한다.

5) 위에 보이는 그림에서 왼쪽이 일반 네트워크이다. 두 개의 네트워크가 깊어지더라고 학습이 잘 되지 않는 것을 볼 수 있다.
6) 34개 층을 갖는 네트워크가 18개 층을 갖는 네트워크보다 오류율(error rate)이 높다.
7) 오른쪽 shortcut이 적용된 네트워크는 레이어가 깊어져도 학습이 잘 되는 효과를 볼 수 있다.
8) 이렇게 학습된 모델은 검증 데이터셋(validation dataset)에서 어떻게 차이가 날지 보기 전에 몇 가지 개념을 알고 가겠다.
(1) Top-1 error란 모델이 가장 높은 확률값으로 예측한 class 1개가 정답과 일치하는지 보는 경우의 오류율이다.
(2) Top-5 error는 모델이 예측한 값들 중 가장 높은 확률값으로부터 순서대로 5개 class 중 정답이 있는지를 보는 것이다.
(3) 이 숫자는 당연히 낮을수록 좋은 것이다.
9) Top-1을 보면 일반 네트워크는 레이어가 18개일 때는 27.94이고, 34개일 때는 28.54로 네트워크가 깊어졌는데도 오류율은 오히려 높아졌다.
10) 경사소실로 인해 훈련이 잘 되지 않았기 때문이다.
11) ResNet에서는 레이어가 18개일 때는 27.88이고, 34개일 때는 25.03으로 레이어가 깊어짐에 따라 오류율이 2.85% 감소했다.
12) 논문에서는 이렇게 간단한 실험으로 Residual Block의 효과를 입증하고 있다.
3. ResNet 이후 시도 (1) Connection을 촘촘히
- ResNet이 보여준 실험결과를 살펴보면 "이 정도 성능이면 충분하지 않을까"라는 생각이 들 수 있지만 개선의 여지는 남아있다.
- DenseNet은 ResNet의 shortcut connection을 마치 Fully Connected Layer처럼 촘촘히 가지도록 한다면 더욱 성능 개선 효과가 클 것이라 생각하고 실험으로 입증했다.
- Dense Connectivity

1) 일반적인 컨볼루션 네트워크가 L개의 레이어에 대해 각 레이어 간 하나씩의 연결, 즉 총 L개의 연결을 갖는 것과는 다르게
2) DenseNet의 기본 블록은 L개의 레이어가 있을 때 레이어 간 L * (L + 1) / 2개의 직접적인 연결(direct connection)을 만든다.
3) 이런 연결구조를 dense connectivity라고 부르며, 아래의 식에서 H로 표기하고 이를 합성함수(composite function)이라 부른다.

4) 각 레이어는 이전 레이어들에서 나온 특성 맵(feature map) 전부를 입력값으로 받는다. 위 식에서 (X0, X1, ..., Xl-1)은 0번째 레이어를 거친 특성 맵부터 l-1번째 레이어를 거친 특성 맵까지를 의미하고,
5) 이들은 합성함수 H를 거쳐 l번째 레이어의 출력값이 된다.
6) DenseNet은 이를 통해서 경사 소실 문제(gradient vanishing)를 개선하고 특성을 계속 재사용할 수 있도록 한다.
7) Shortcut connection이 있어 ResNet과 비슷해보일 수 있지만 ResNet은 shortcut을 원소별로 단순히 더해주었던 반면,
8) DenseNet은 하나하나를 차원으로 쌓아서(concatenate) 하나의 텐서로 만들어 낸다는 사실이 다르다.
9) 또 이전 ResNet의 connection에 다른 연산이 없었던 것과 달리, 합성함수 H은 이 텐서에 대해 배치 정규화(batch normalization, BN), ReLU 활성화 함수, 그리고 3x3 컨볼루션 레이어를 통해서 pre-activation을 수행한다.

10) Pre-activation 개념은 Identity Mappings in Residual Networks 논문에서 제시되었는데, 위 그림의 (b)에서 보듯이 ReLU가 컨볼루션 블록 안으로 들어간 것을 의미한다.
- Growth Rate
1) 특성 맵을 더해주던 ResNet과 달리 DenseNet에서는 특성 맵을 채널 방향으로 쌓아서 사용한다.
2) 그렇다면 4개의 채널을 가진 CNN레이어 4개를 DenseNet 블록으로 만들었을 때, 입력값의 채널 갯수가 4인 경우 블록 내 각 레이어의 입력값은 몇 개 채널을 가질까?
3) 첫 번째 레이어 입력값의 채널은 입력 데이터의 채널 그대로 4이다.
4) 두 번째 레이어의 입력값은 입력 데이터의 채널값과, 첫 번째 레이어 출력값의 채널인 4을 더해 8이 된다.
5) 세 번째 레이어는 입력 데이터의 채널 4와 첫 번째 레이어 출력값 채널 4, 두 번째 레이어 출력값의 채널 4를 받아 12개의 특성맵을 입력 받고, 네 번째 레이어는 같은 방식으로 16개의 특성 맵을 입력받는다.
6) 입력값이 채널 4로 시작했으나 진행할수록 특성 맵의 크기가 매우 커지는 것을 볼 수 있다.
7) 이를 제한하기 위해서 논문에서는 growth rate라는 값을 조정하여 레이어를 거치면서 증가하게 되는 채널의 갯수를 조절한다.
8) 위의 예시에서 CNN의 채널 수를 4로 정햇는데 이것이 growth rate라 할 수 있다.
9) 블록 내의 채널 개수를 작게 가져가면서 최종 출력값의 특성 맵 크기를 조정할 수 있도록 했다고 한다.
10) 이외에도 여러 방식이 적용되었으니 DenseNet Tutorial 1 Paper Review & Implementation details 에서 bottleneck 레이어, transition 레이어, composite function 등에 대해 살펴보면 좋다.
4. ResNet 이후 시도 (2) 어떤 특성이 중요할까?
- 네트워크 구조를 연달아 다루어 많이 힘들 수 있다. 오늘의 마지막 네트워크 SENet을 살펴보겠다.
- SENet은 Squeeze-and-Excitation Networks의 줄임말이다. 어떤 것을 squeeze and excite 할까?
- 일반적인 CNN은 입력에 대해서 컨볼루션 필터를 필터 사이즈(filter size)에 따라 적용한다.
- 이 때 필터의 갯수가 곧 컨볼루션 레이어 출력값의 채널 갯수가 된다.
- SqueezeNet에서는 이 때 채널 방향으로 global average pooling을 적용, 압축된 정보를 활용하여 중요한 채널이 활성화되도록 한다.
- 어떻게 보면 CNN에서 나온 특성맵의 채널에 어텐션(attention) 매커니즘을 적용한 블록을 만들었다고 볼 수 있다.
- Squeeze
1) Squeeze는 말 그대로 특성에서 중요한 정보를 짜내는 과정이다.
2) 특성 맵의 채널에서 어느 채널이 중요한지 정보를 만들기 위해서는 우선 채널에 따른 정보를 압축해서 가져와야 한다.
3) 어떻게 채널별 정보를 압축할 수 있을까?
4) 일반 CNN에서도 많이 사용하듯, 풀링(pooling) 기법을 사용하면 된다. 풀링은 보통 커널(kernel) 영역의 정보를 압축하는데 사용한다.
5) 커널 영역에 대해 최댓값만 남기는 것이 Max Pooling, 평균값을 남기는 것이 Average Pooling이다.

6) 위 그림을 살펴보면 Squeeze는 Fsq 함수에서 일어난다.
7) Ftr이라는 컨볼루션 레이어를 커치면 HxWxC의 크기를 가진 특성 맵 U가 나온다.
8) U에 Squeeze를 적용하면 1x1xC의 크기가 나오게 된다.
9) 벡터의 차원으로 볼 수 있듯이 각 채널별로 딱 1개의 숫자만 남도록 2D 특성맵 전체에 대해 평균값을 남기는 global average pooling을 수행한다.
10) 이렇게 얻어진 1x1xC의 벡터는 채널별 정보를 압축해 담고 있다.
- Excitate
1) 채널별 정보를 짜내는데 성공했다. 이제 채널별 정보에 따라 어떤 채널을 강조해야 할지 판단하면 된다.
2) 채널을 강조하는 것을 논문에서는 excitation으로 표현하며, 수식은 아래와 같다. 이전에 봤던 전체 네트워크 그림의 Fex식이다.

3) 수식은 매우 부담스럽게 생겼지만 하나씩 살펴보자.
(1) z는 위에서 global average pooling을 적용한 특성, 즉 squeeze 활동의 결과물이다.
(2) 이 특성에 W1을 곱해주는 linear 레이어를 거치고 ReLU 활성화 함수 δ를 거친다.
(3) 이후 두 번째 W2를 곱해주는 linear layer를 거치고 마지막으로 시그모이드(sigmoid) 활성화 함수 σ를 거친다.
4) 이 때 시그모이드를 사용하는 이유는 가장 중요한 하나의 채널만 활성화되는 것이 아닌, 여러 채널들이 서로 다른 정도로 활성화되도록 하기 위함이다.
5) 데이터셋에 정답 라벨이 하나뿐인 단순 분류 모델의 활성화 함수로는 소프트맥스(SoftMax)를 사용해서 단 하나의 최댓값을 찾지만,
6) 하나의 대상에도 여러 개의 클래스의 정답 라벨을 지정할 수 있는 다중 라벨 분류(multi label classification)에서는 시그모이드를 사용하는 것과 같은 방식이다.
7) 이렇게 계산된 벡터를 기존의 특성 맵에 채널에 따라서 곱해주어 중요한 채널이 활성화 되도록 만들어 준다.

5. 모델 최적화하기 (1) Neural Architecture Search
- 지금까지 봤던 방법은 사람이 고안한 방식을 네트워크 구조에 적용하여 효과를 봤던 방법이다.
- 모델의 훈련은 컴퓨터가 시켜줄 수 있어도, 어떤 모델 구조가 좋을지는 사람이 직접 고민하고 실험해 보아야 한다.
- 이렇게 새로운 모델 구조를 고안하고 이해하는 과정을 반복하다 보면, "우리가 딥러닝으로 이미지 분류 문제를 풀기 위해 딥러닝 모델의 파라미터(parameter)를 최적화해 왔듯이 모델의 구조 자체도 최적화 할 수 없을까?"라고 생각할 수 있다.
- 이렇게 여러 가지 네트워크 구조를 탐색하는 것을 아키텍쳐 탐색(architecture search)라고 한다.
- 그리고 그 중 신경망을 사용해 모델의 구조를 탐색하는 접근방법을 NAS(neural architecture search)라고 한다.
- NASNet은 NAS에 강화학습을 적용하여 500개의 GPU로 최적화한 CNN 모델들이다.
- 직접 모델 탐새을 할 환경을 구축하지 않더라도 텐서플로우에서 이미지넷 2012년 데이터셋에 최적화된 구조의 pre-trained NASNet 모델을 쉽게 사용할 수 있다.
- 그럼 NasNet은 어떤 방법으로 만들어졌는지 대략적으로 살펴보자
- NASNet
1) NASNet과 같이 거창한 방법이 아니더라도, 일반적으로 머신러닝에서는 그리드 탐색(grid search) 등으로 실험과 모델 세팅(config)를 비교하기 위한 자동화된 방법을 사용하곤 한다.
2) 그리드 탐색은 간단히 말해서 주어진 모든 조합을 실험해 보는 것이다.
3) 그러나 그리드 탐색과 같은 방법으로 접근할 경우 모델에서 바꿔볼 수 있는 구성의 종류가 매우 많아서 머신 러닝 중에서도 학습이 오래 걸리는 딥러닝에서는 적합하지 않다.
4) 딥러닝에서 모델을 탐색하기 위해 강화학습 모델이 대상 싱견망의 구성(하이퍼파라미터)을 조정하면서 최적의 성능을 내도록 하는 방법이 제안되었으며, NASNet은 그 중 하나이다.
5) 아키텍쳐 탐색을 하는 동안 강화학습 모델은 대상 신경망의 구성을 일종의 변수로 조정하면서 최적의 성능을 내도록 한다.
6) 우리가 지금까지 봤던 레이어의 세부 구성, CNN의 필터 크기, 채널의 갯수, connection 등이 조정할 수 있는 변수가 된다.
7) 이렇게 네트워크 구성에 대한 요소들을 조합할 수 있는 범위를 탐색 공간(search space)이라고 한다. 이 공간에서 최고의 성능을 낼 수 있는 요소의 조합을 찾는 것이다.
8) NASNet이 NAS를 처음 적용한 것은 아니며 이전에도 논문은 있었다.
9) 이전의 방식들은 우리가 많이 접해왔던 MNIST에 최적화하는데 800개의 GPU를 사용해서 28일이 걸렸다고 한다. 그렇게 나온 구조가 아래의 그림이다.
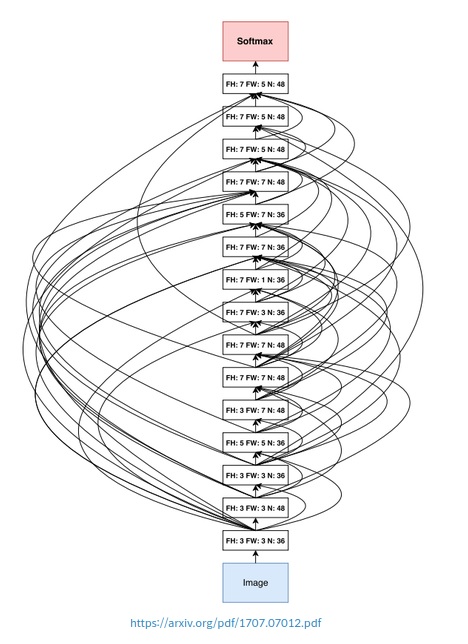
10) NASNet 논문은 이미지넷 데이터에 대해 이보다 짧은 시간 안에 최적화를 했다고 한다. 어떻게 한 것일까?
- Convolution cell

1) 레이어 하나마다의 하이퍼 파라미터를 조절한다면 탐색 공간이 무지막지 방대해질 것이다.
2) 탐색공간이 넓다는 말은 찾아야 할 영역이 넓다는 의미이고 넓은 곳에서 최적의 포인트를 찾는 데는 당연히 더 오랜 시간이 걸릴 것이다.
3) NASNet 논문에서는 이런 탐색공간을 줄이기 위해서 모듈(cell) 단위의 최적화를 하고 그 모듈을 조합하는 방식을 채택했다.
4) ResNet에는 Residual Block, DenseNet에는 Dense Block이라는 모듈이 사용됬는데, 논문에서는 이와 유사한 개념을 convolutuin cell이라 부른다.
5) Convolution cell은 normal cell과 reduction cell로 구분된다.
6) Normal cell은 특성 맵의 가로, 세로가 유지되도록 stride를 1로 고정한다.
7) Reduction cell은 stride를 1 또는 2로 가져가서 특성 맵의 크기가 줄어들 수 있도록 한다.
8) 논문의 모델은 normal cell과 reduction cell 내부만을 최적화하며, 이렇게 만들어진 convolution cell이 위 그림의 두 가지이다.
9) 두 가지 cell을 조합한 것이 최종 결과 네트워크(NASNet)을 만들었으며, 좀 더 적은 연산과 가중치로 SOTA(state-of-the-art) 성능을 기록했다고 한다.
6. 모델 최적화하기 (2) EfficientNet
- 이번에 살펴볼 접근방법은 2019년에 발표된 EfficientNet이다.

- EfficientNet의 강력함은 위의 그래프로 한눈에 볼 수 있다.
- 기존 모델들의 오류율을 뛰어넘을 뿐 아니라 모델의 크기인 Number of Parameters 또한 최적화 된 것을 볼 수 있다.
- 빨간색 선이 EfficientNet의 모델들이고 그 아래로 각 점에 따라서 이전에 봐왔던 모델들이 있는 것을 볼 수 있다.
- 정확도를 얻는데 다른 네트워크는 무지막지한 파라미터의 수를 사용하는데 EfficientNet은 작고 효율적인 네트워크를 사용했다고 볼 수 있다.
- EfficientNet은 우리가 이미지에 주로 사용하는 CNN을 효율적으로 사용할 수 있도록 네트워크 형태를 조정할 수 있는 width, depth, resolution 세 가지 요소에 집중한다.
- 여기서 width는 CNN의 채널에 해당한다. 채널을 늘려줄수록 CNN의 파라미터와 특성을 표현하는 차원의 크기를 키울 수 있다.
- depth는 네트워크의 깊이이다. ResNet은 대표적으로 네트워크를 더 깊게 만들 수 있도록 설계해 성능을 올린 예이다.
- 마지막으로 resolution은 입력값의 너비(w)와 높이(h) 크기이다. 입력이 클수록 정보가 많아져 성능이 올라갈 여지가 생기지만 레이어 사이의 특성 맵이 커지는 단점이 있다.
- Compound scaling
1) EfficientNet은 앞서 말한 resolution, depth, width를 최적으로 조정하기 위해서 앞선 NAS와 유사한 방법을 사용해 기본 모델(baseline network)의 구조를 미리 찾고 고정해둔다.
2) 모델의 구조가 고정이 되면 효율적인 모델을 찾는다는 커다란 문제가 개별 레이어의 resolution, depth, width를 조절해 기본 모델을 적절히 확장시키는 문제로 단순해진다.

3) 그리고 EffientNet 논문에서는 resolution, depth, width라는 세 가지 scaling factor를 동시에 고려하는 compound scaling을 제안한다.
4) 위의 식에서 compound coefficient Φ는 모델의 크기를 조정하기 위한 계수가 된다.
5) 위 식을 통해 레이어의 resolution, depth, width를 각각 조정하는 것이 아니라 고정된 계수 Φ에 따라서 변하도록 하면 보다 일정한 규칙에 따라(in a principled way) 모델의 구조가 조절되도록 할 수 있다.
6) 논문은 우선 Φ을 1로 고정한 뒤 resolution, depth, width을 정하는 α, β, γ, 즉 resolution과 depth, width의 기본 배율을 고정한 뒤 compound coefficient Φ를 조정하여 모델의 크기를 조정한다.
'공부 > AIFFEL' 카테고리의 다른 글
| Going Deeper(CV)_DJ 3 : 잘 만든 Augmentation, 이미지 100장 안 부럽다 (0) | 2021.04.09 |
|---|---|
| Going Deeper(CV)_DJ 2 : 없다면 어떻게 될까? (ResNet Ablation Study) (2) | 2021.04.07 |
| 2021년 3월 31일 모두의 연구소(인공지능 전문가 과정) - 63일차 (0) | 2021.03.31 |
| 2021년 3월 30일 모두의 연구소(인공지능 전문가 과정) - 62일차 (0) | 2021.03.31 |
| 2021년 3월 29일 모두의 연구소(인공지능 전문가 과정) - 61일차 (0) | 2021.03.29 |