1. Regulrization과 Normalization
- Regularization? Normalization?
1) 위 두 개념은 서로 헷갈리는 경우가 많다. 한국어로 변역할 때 두 개념이 다 "정규화"로 번역될 때가 많아서 더욱 혼란스럽다.
2) Regularization
(1) 오버피팅을 해결하기 위한 방법 중 하나이다.
(2) L1 / L2 Regularization, Dropout, Batch normalization등이 있다.
(3) 이 방법들은 모두 오버피팅을 해결하고자 하는 방법이다.
3) Normalization
(1) 데이터의 형태를 좀더 의미있게, 혹은 트레이닝에 적합하게 전처리하는 과정이다.
(2) 데이터를 z-score로 바꾸거나, minmax scaler를 사용하여 0과 1사이의 값으로 분포를 조정하는 것들이 해당된다.
(3) 학습 초반에 데이터 거리간의 측정이 피처 값의 범위 분포 특성에 의해 왜곡되어 학습에 방해를 받게 되는 경우가 있는데
(4) Normalization은 이를 모든 피처의 범위 분포를 동일하게 하여 모델이 풀어야 하는 문제를 좀 더 간단하게 바꿔주는 전처리 과정이다.
4) 정리하자면, Regularization은 오버피팅을 막고자 하는 방법, Normalization은 트레이닝을 할 때에 서로 범위가 다른 데잍터들을 같은 범위로 바꿔주는 전처리 과정이다.
2. L1 Regularization
- L1 Regularization(Lasso)의 정의
1) 라쏘의 식을 보면 (람다 + 절대값)이 있는 부분이 있는데 이 부분이 없다면 Linear Regression과 동일하다. 이 부분이 중요한 점이다.
2) 이 부분에서 L1라는 이름이 붙은 이유가 나타나기도 하고, L2와의 차이를 나타내는 중요한 부분이다.
3) 참고 지식
(1) Lp norm : norm은 벡터나 행렬, 함수 등의 거리를 나타내는 것으로 우리는 여기서 벡터값만 다룬다.
- 이전 스텝에서 왜 L1 Regularization 만 답이 나오지 않았을까?
1) 이전 스텝에서 Linear와 L1, L2를 가지고 선형관계 그래프를 그렸을 때 L1만 기울기가 0으로 나왔다. (기울기가 0으로 나오면 안되는 데이터였다.)
2) 여러 복잡한 수식을 거치는데 이해는 못해서 패스했다.
3) p = 1인 경우 β0에 대해 미분하는 과정에서 람다가 사라지므로 Regularization의 효과를 볼 수 없다고 한다.
4) X가 1차원 값인 선형회귀분석 같은 경우에는 L1 Regularization이 의미가 없다는 것을 말한다. 그러므로 L1 Regularization을 사용할 때는 X가 2차원 이상인 여러 컬럼 값이 있는 데이터일 때 실제 효과를 볼 수 있다한다.
3. L2 Regularization
- L2 Regularizatio(Ridge)의 정의
1) 식을 보면 (람다 + β^2) 부분이 L1과차이가 있는 것을 알 수 있다.
- 아래 그림은 수식 없이 직관적인 이해를 좀 더 요구하는 그림이다.
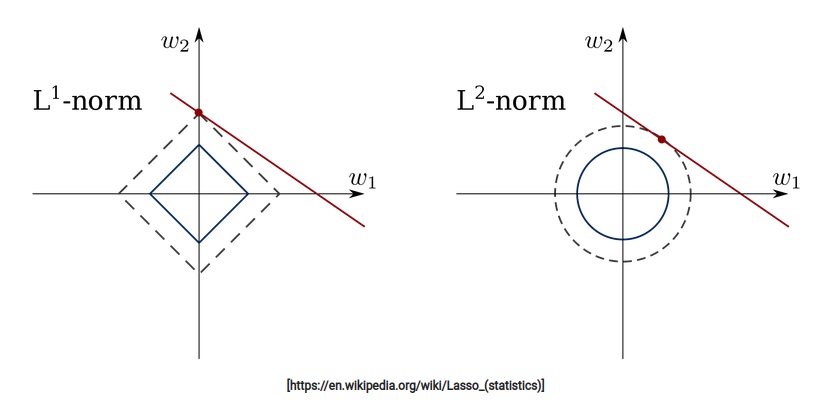
1) L1은 |β|를 이용하여 마름모형태의 제약조건이 생긴다.
2) 그리고 위 등고선처럼 보이는 내용은 우리가 풀어야 하는 문제이다.
3) 이 문제가 제약조건과 만나는 지점이 해가 된다.
4) 그래서 L1에서는 몇 개의 축에서 β값을 0으로 보낸다.
5) 반면 L2는 β^2이므로 원의 형태로 나타나게 된다.
6) 그러므로 0에 가지는 않고 0에 가깝게 감을 확인할 수 있다.
7) 또한 제곱이 들어가 있기 때문에 절대값을 쓰는 Lasso보다는 수렴이 빠르다는 장점이 있다.
- 정리하면
1) L1은 가중치가 적은 벡터에 해당하는 계수를 0으로 보내면서 차원축소와 비슷한 역할을 하는 것이 특징이다.
2) L2는 0이 아닌 0에 가깝게 보내지만 제곱 텀이 있기 때문에 L1보다는 수렴 속도가 빠르다는 장점이 있다.
4. Extra : Lp norm
- Norm이라는 개념은 벡터뿐만 아니라 함수, 행렬에 대해서 크기를 구하는 것으로, 딥러닝을 배우는 과정에서는 주로 벡터, 좀 더 어렵게는 행렬의 Norm 정도만 알면 된다.
- vector norm
1) L1 / L2에서 배운 Norm은 벡터에서 사용한 Norm이다.
- matrix norm
1) 행렬의 norm의 경우는 벡터와 조금 다르며, 주로 p = 1, inf인 경우만 알면 된다.
2) p = 1인 경우에는 컬럼의 합이 가장 큰 값이 출력되고, p = inf인 경우에는 로우의 합이 가장 큰 값이 출력된다.
5. Dropout
- 드롭아웃(Dropout) 기법은 2014년도에 나온 논문이다.
- 드롭아웃 기법이 나오기 전의 신경망은 fully connected architecture로 모든 뉴런들이 연결되어 있었다.
- 그러나 드롭아웃이 나오면서 확률적으로 랜덤하게 몇 가지의 뉴런만 선택하여 정보를 전달하는 과정이다.
- 이름 그대로 몇 가지의 값들을 모든 뉴런에 전달하는 것이 아닌 확률적으로 버리면서 전달하는 기법이다.
- 드롭아웃은 오버피팅을 막는 Regularization layer 중 하나이다.
- 확률을 너무 높이면, 제대로 전달되지 않으므로 학습이 잘 되지 않고,
- 확률을 너무 낮추면, fully connected layer와 같다.
- fully connected layer에서 오버피팅이 생기는 경우에 주로 Dropout layer를 추가한다.
- 코드는 간단하다. 논문이 나온 지도 오래되었기 때문에, 여러 프레임워크에서 간단하게 구현할 수 있도록 되어있다.
6. Batch Normalization
- Batch Normalization은 gradient vanishing, explode 문제를 해결하는 방법이다.
- 논문 제목은 Batch Normalization : Accelerating Deep Network Training by Reducing Internal Covariate Shift (2015) 이다.
- 여기 논문의 알고리즘을 보면 아래와 같은 식이 있다.

1) 수식에서 중요한 부분은 normaliza 부분에서 분모가 ε이 추가되었다는 점이다.
2) 이 부분으로 인해 normaliza 과정에서 gradient가 사라지거나(vanishing), 폭등하는(explode) 것을 막을 수 있다.
3) ε 부분만 제외하면, 기존의 z-score로 normaliza하는 과정과 같지만, 이 부분을 추가하는 것만으로도 오버피팅이나 학습이 잘 되지 않는 것을 막을 수 있게 된다.
'공부 > AIFFEL' 카테고리의 다른 글
| 2021년 3월 24일 모두의 연구소(인공지능 전문가 과정) - 59일차 (0) | 2021.03.24 |
|---|---|
| Exploration 20 : 난 스케치를 할 테니 너는 채색을 하거라 (0) | 2021.03.23 |
| FUNDAMENTAL 32. Likelihood(MLE와 MAP) (0) | 2021.03.19 |
| Exploration 19 : 인간보다 퀴즈를 잘 푸는 인공지능 (0) | 2021.03.18 |
| FUNDAMENTAL 31. Ainize, 나의 원클릭 포트폴리오 만들기 (0) | 2021.03.17 |